Complex System Science
 I am currently engaged in utilizing the information dynamics approach to understand airline dynamics. Recently, we investigated the reconstruction of the "functional complex networks", and I have prepared a blog post based on the findings.
I encourage you to read the article, which is freely available, along with the blog post. In the forthcoming days, I will share more results as soon as they become available to the public.
Besides, I am eager to share with you three projects I have undertaken in the past. Allow me to briefly introduce my three distinct projects, each exploring a unique aspect of complex systems science.
I am currently engaged in utilizing the information dynamics approach to understand airline dynamics. Recently, we investigated the reconstruction of the "functional complex networks", and I have prepared a blog post based on the findings.
I encourage you to read the article, which is freely available, along with the blog post. In the forthcoming days, I will share more results as soon as they become available to the public.
Besides, I am eager to share with you three projects I have undertaken in the past. Allow me to briefly introduce my three distinct projects, each exploring a unique aspect of complex systems science.
(1): Transfer Entropy in Non-Linearly Coupled Rössler Systems
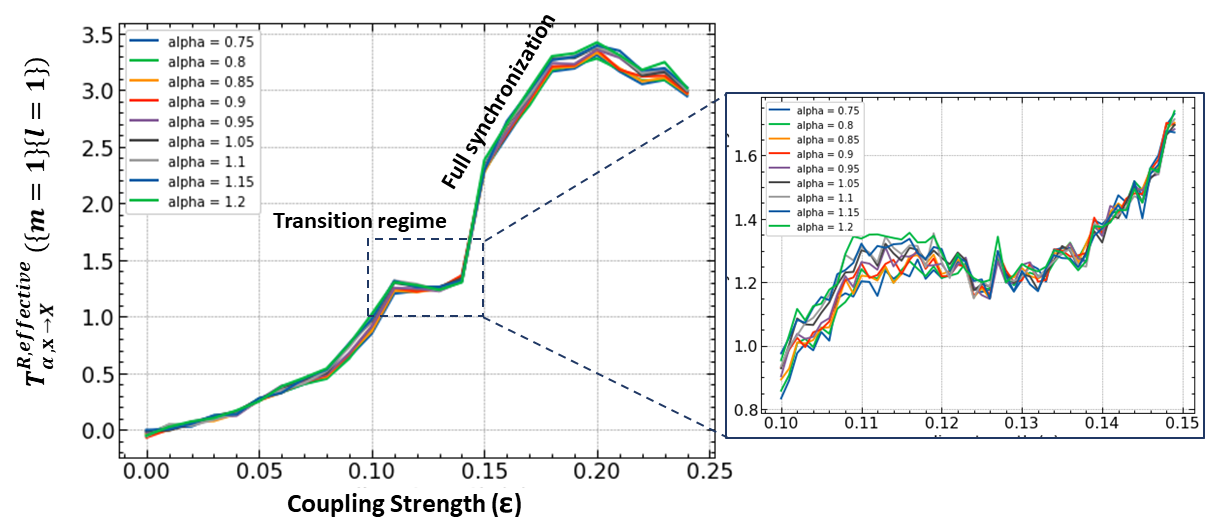
Complex systems, often exhibiting properties like phase transitions, emergent behaviors, synchronization, and non-linear dynamics, necessitate an understanding of information generation, storage, and transfer across subsystems. Traditional techniques like cross-correlation and Granger causality prove inadequate for non-linear interactions, prompting the adoption of Transfer Entropy (TE) and Renyi entropy to capture non-Gaussian and non-linear characteristics. This project employs Renyi Transfer Entropy (RTE) to investigate the dynamics of two coupled non-linear Rössler systems en route to synchronization, demonstrating RTE's efficacy in studying information transfer in non-linearly coupled chaotic systems and its potential applicability in other real-world chaotic systems.
(2): The Langevin Approach for Modeling Markov Processes: Extracting Model Equations from Data
Standard statistical tools, while useful for capturing essential features of a stochastic data series, Probability Density Function (PDF), cannot fully reveal the underlying dynamics of the system. The Langevin Approach, which facilitates the extraction of stochastic evolution equations from sets of measurements, offers a deeper understanding of systems dynamics. In this project, a Python code has been developed to analyze one- and two-dimensional time series and estimate drift and diffusion coefficients that describe the deterministic and stochastic components of the analyzed process. By numerically integrating Langevin processes, the results can be cross-checked, and synthetic data sets can be generated, highlighting the ability of the Langevin evolution equation to uncover complex dynamics even when associated statistics resemble other stochastic processes.
(3): Exploring the Culture Space: Cultural Transmission and Evolution of Cultural Complexity
Developed during the "Winter School Evolution of Social Complexity, 2022," this project uses data from the Seshat databank to create computer-generated multidimensional spaces of cultural variables, examining how different polities navigated these "culture spaces" over centuries. Employing large cross-cultural databases and computational modeling approaches, this study aims to expand our understanding of the patterns and processes that shaped human cultural evolution. The work is ongoing.
Plasma Physics
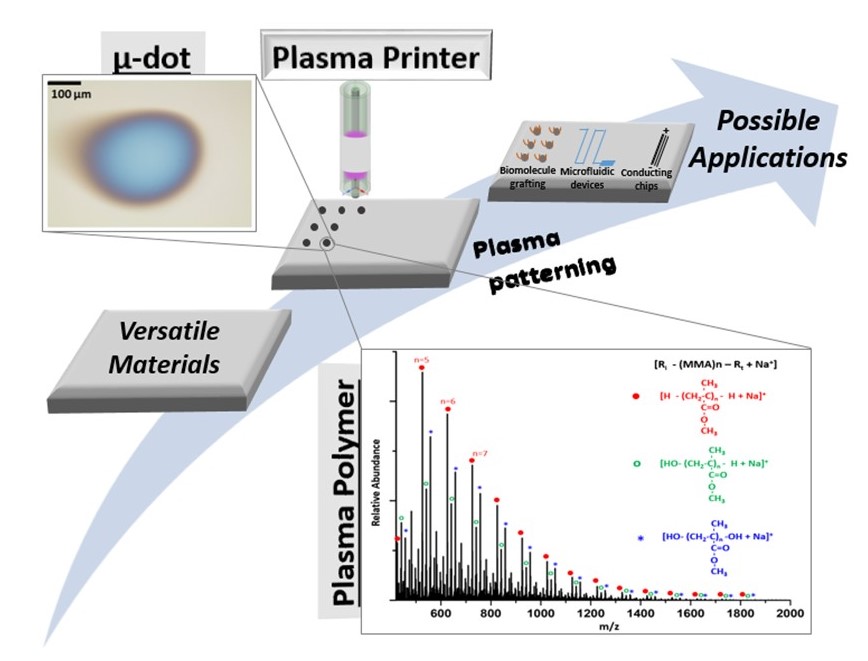 Non-thermal plasma, characterized by distinct temperatures of charged particles and neutral species, has gained attention due to its unique properties and potential applications.
The studies explore different aspects of non-thermal plasma, shedding light on its behavior and possible uses.
Non-thermal plasma, characterized by distinct temperatures of charged particles and neutral species, has gained attention due to its unique properties and potential applications.
The studies explore different aspects of non-thermal plasma, shedding light on its behavior and possible uses.
- Plasma-Surface Interaction Study - Investigating a low-temperature helium plasma jet at atmospheric pressure, this study employs Mueller polarimetry to examine the jet's impact on an electro-optic target's electric field and temperature. The research highlights the method's precision in detecting minute temperature changes and electric field evolution due to charge accumulation on the target. Findings reveal that within a 20 to 50 kHz frequency range, the plasma maintains stable ionization waves and a consistent temperature rise, with minimal charge deposition and significant surface area expansion. Additionally, a subtle heat exchange within the plasma plume is observed, offering insights into plasma behavior and its interaction with dielectric surfaces under specific conditions.
- Plasma Printing - This research utilizes non-equilibrium plasma in a process called Plasma Enhanced Chemical Vapor Deposition (PECVD) to create thin films. It aims to enhance Additive Manufacturing (AM) by providing high-resolution, selectively localized coatings using Atmospheric Pressure PECVD (AP-PECVD). The study demonstrates the potential of AP-PECVD in AM, showcasing a lab-created plasma device that can vary the size of the deposited material by adjusting the injector's dimensions, highlighting non-thermal plasma's role in refining manufacturing techniques.
Fluid Dynamics
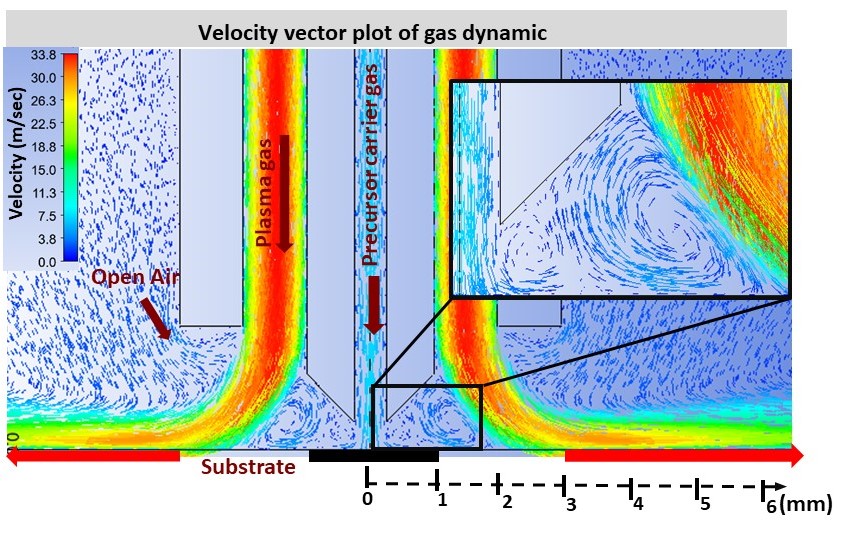 Computational Fluid Dynamics (CFD) is a powerful technique for analyzing fluid flow behavior in various contexts, including non-thermal plasma behavior in Atmospheric Pressure Plasma Enhanced Chemical Vapor Deposition (AP-PECVD) processes.
By employing CFD simulations, interdisciplinary research can uncover the crucial role of gas flow dynamics in the deposition process, encompassing reactive plasma species, precursor molecules, and their interactions with the substrate surface.
Computational Fluid Dynamics (CFD) is a powerful technique for analyzing fluid flow behavior in various contexts, including non-thermal plasma behavior in Atmospheric Pressure Plasma Enhanced Chemical Vapor Deposition (AP-PECVD) processes.
By employing CFD simulations, interdisciplinary research can uncover the crucial role of gas flow dynamics in the deposition process, encompassing reactive plasma species, precursor molecules, and their interactions with the substrate surface.
- Kinetic Regimes - This study unveils three distinct kinetic regimes in atmospheric pressure plasma torch deposition, crucial for achieving specific coating morphologies like no deposition, circular dots, and rings. By modulating the gas flow rate, one can tailor the deposition's size and shape within a designated zone, underscoring the gas flow's pivotal role in the AP-PECVD process. This insight, supported by experiments and computational fluid dynamics simulations, demonstrates how gas flow dynamics and precursor mixing influence the final coating characteristics, enhancing our understanding and control of plasma-based coating applications.
- Plasma Enhanced Chemical Vapour Deposition - This research establishes a link between the deposition patterns of organosilicon compounds and plasma species distributions, using computational fluid dynamics (CFD) to predict outcomes in AP-PECVD. By altering plasma species distribution, the study shows how one can influence the chemical properties and deposition patterns, crucial for targeted applications in additive manufacturing. The experiments with different organosilicon precursors demonstrate varied deposition rates and patterns, attributing to the presence of vinyl or ethoxy groups. This work underscores the importance of understanding plasma species behavior to refine AP-PECVD processes, offering profound insights for area-selective coating in advanced manufacturing.